Objektiivin aukon merkitys
Tämän sarjan kahdessa ensimmäisessä artikkelissa olen kertonut hiukan siitä, miten kameran objektiivia voidaan tietyssä mielessä tarkastella vastaavana yhden linssin systeeminä, ja että miksi objektiivit eivät kuitenkaan koostu yleensä vain yhdestä linssistä. Kummassakin artikkelissa mainitsin objektiivin aukon koon – tai vaihtoehtoisesti objektiivin aukkoluvun. Tässä kolmannessa osassa paneudun hiukan tähän objektiivin aukkoon, joka on useimmiten eri asia kuin linssien läpimitta.
Aukkoluku
Jo ensimmäisessä osassa minulla oli piirrettynä objektiivin aukko yksinkertaistetussa objektiivin mallissa – silloin käytin samaa kuvaa, kun nyt alla oleva kuva1.
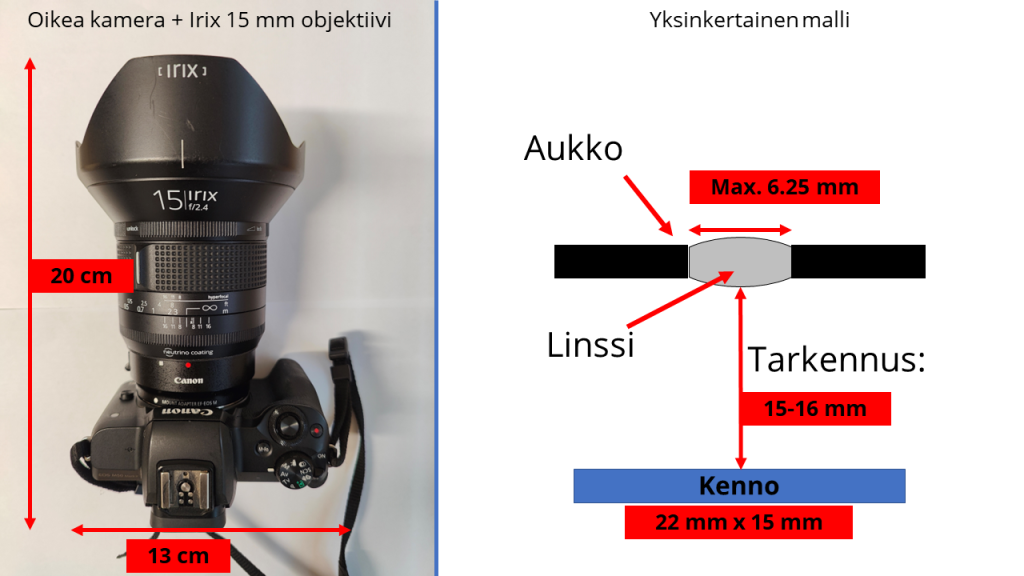
Siinä oikealla puolella on objektiivia vastaava yhden linssin malli, ja linssin koko on siinä käytännössä sen mallin aukko. Kamerassahan suurin aukko merkitään usein merkinnällä tyyliin $f/2.5$ tai $f:2.5$, jolloin tarkoitetaan, että objektiivin polttovälin $f$ suhde suurimpaan käytettävissä olevaan aukon kokoon on $f/D$. Ja tätä kutsutaan aukkoluvuksi.
Järjestelmäkameroissa tätä aukkolukua voidaan säätää. Käytännössä se tapahtuu objektiivin sisällä olevaa fyysistä aukkoa suurentamalla tai pienentämällä. Kaikissa kameroissa tätä mahdollisuutta ei ole. Yleensä kännyköissä ja action-kameroissa aukko on kiinteästi jotain. Tämä yksinkertaistaa ja pienentää objektiivin kokoa, mutta samalla jättää yhden kuvan säätämisen mahdollisuuden pois.
Mutta mitä vaikutusta aukon koolla sitten on? Tämänkin analysointi on aika yksinkertaista tiettyyn pisteeseen asti. Lähdetään tarkastelemaan tätä kuvan 2 avulla. Siinä olen piirtänyt kuvattavan kohteen (tähti) ja sen kuvan yksinkertaisen linssin tapauksessa. Ja tällaiselle aukko on siis kyseisen linssin koko.
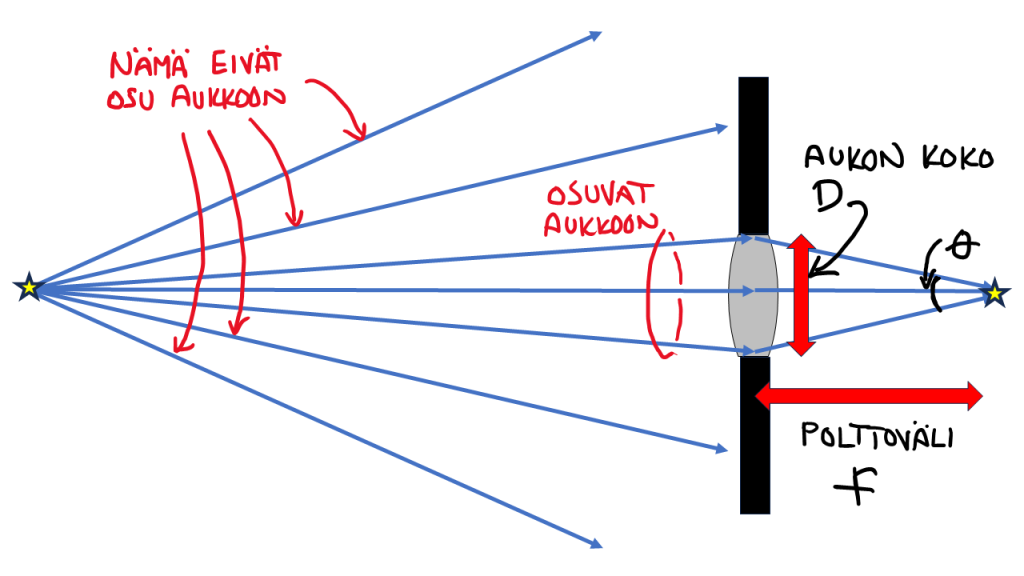
Kuvattava kohde näkyy siksi, että se joko säteilee valoa itse tai sitten se heijastaa ympäröivää valoa. Kummassakin tapauksessa lähes aina valoa leviää hyvin laajalle alueelle. Ja yksinkertaisesti se valo, joka osuu objektiivin aukkoon, pääsee päätymään kuvatasolle, eli siis kameran kennolle. Jos kuvittelemme vaikka pyöreän aukon, jonka läpimitta on $D$, niin objektiiviin läpi kulkevan valon määrä riippuu aukon pinta-alasta, eli on verrannollinen $D$:n toiseen potenssiin.
Joten yksinkertaisesti: Kameraan päätyvän valon määrä riippuu siitä, mikä on aukon koko. Ja jos käytämme valokuvaa ottaessa objektiivia, jolla on joku tietty polttoväli $f$, niin aukkoluvun kasvattaminen (eli aukon suurentaminen) lisää kameran kennolle päätyvän valon määrää.
Joskus tulevaisuudessa kirjoittanen sitten oman artikkelin siitä, miten kameran kuvan ottamisen säädöt eli aukkoluku, valotusaika, ja herkkyys riippuvat toisistaan. Mutta jo sen verran voin kertoa tästä yksinkertaisesta logiikasta sen, että aukkoluvun pienentäminen, eli aukon koon kasvattaminen lyhentää tarvittavaa valotusaikaa, koska silloin pääsee objektiivin läpi enemmän valoa.
Eli kuvan 2 vasen puoli oli yksinkertainen. Oikea puoli on sitten vähän haastavampi, koska sen vaikutus ei ole todellisissa tapauksissa niin yksinkertainen. Mutta pitkähkön teoreettisen lähestymisen voi kiteyttää seuraavaan:
Kuvitellaan, että meillä on täydellinen objektiivi, jossa ei ole minkäänlaisia vääristymiä. Ja jo heti voidaan todeta, että eihän tällaisia oikeasti ole olemassa, kuten jo sarjan toisessa osassa totesin. Mutta kuvitellaan nyt kuitenkin tällainen tapaus, ja katson myöhemmin, että mitä tapahtuu todellisessa tapauksessa.
Täydelliselle linssille voidaan johtaa yksinkertainen lauseke sille, miten pieneksi pisteeksi se voi kuvata äärettömän kaukana olevan pistemäisen kohteen. Siis konkreettisesti: jos kuvaamme taivaalla olevaa tähteä (joka normaalin kameran näkökulmasta on piste), niin miten pieni voi pienimmillään olla sen kuva kennolla. Ja tämän antaa likimain lauseke:
$$ x \approx 1.22 \lambda \frac{f}{D}, $$
missä $x$ on kyseisen kuvapisteen läpimitta $\approx$ tarkoittaa, että on likimain yhtä suuri, $\lambda$ tarkoittaa tarkasteltavaa (yhtä) valon aallonpituutta, ja $\frac{f}{D}$ on tuo aiemmin mainitsemani aukkoluku. Tätä pisteen ideaalista kuvaa kutsutaan Airyn kuvioksi. Se on siis tietyn muotoinen valoläiskä, jonka läpimitta on likimain kyseinen $x$. Myöhemmin näytän muutaman simulointikuvan objektiiveista, ja niissä olen piirtänyt ”Airy-renkaan,” joka on rengas, jonka läpimitta on kyseinen $x$. Eli se kuvaa sitä, miten iso olisi ideaalisesti kyseinen pisteen kuva.
Aukon määräämällä pienimmällä mahdollisella pistemäisen kohteen kuvan koolla, eli Airyn kuvion koolla, on myös tärkeä merkitys kuvan tarkkuudessa. Nimittäin, se antaa parhaan mahdollisen kulmatarkkuuden. Tämän kulmatarkkuuden periaatetta olen hahmotellut kuvassa 3.
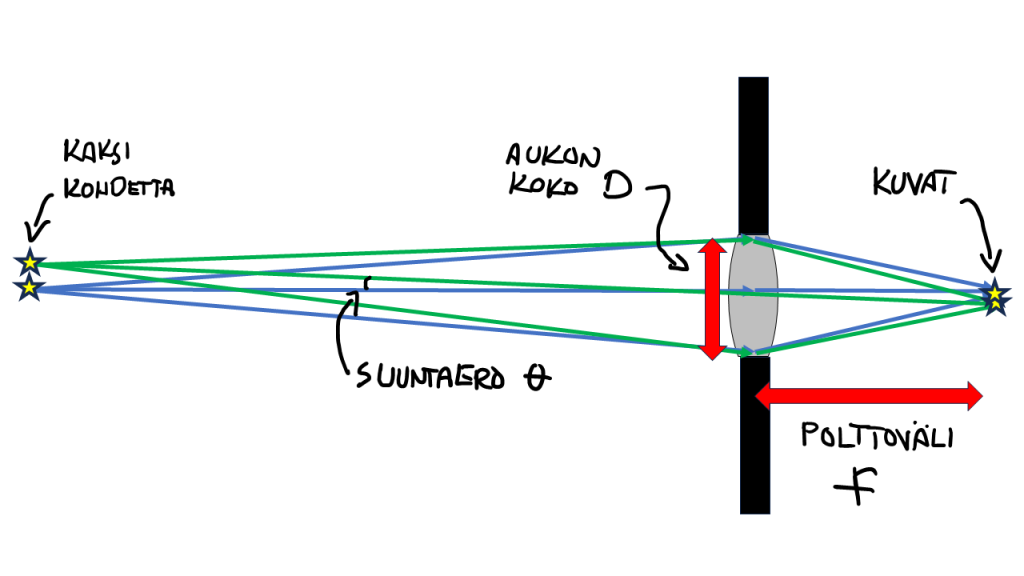
Kyse on siitä, että jos katsotaan tai kuvataan kahta pistemäistä lähdettä, kuten tähtiä taivaalla, niin on olemassa pienin mahdollinen suuntaero $\theta$, jolla kyseiset kohteet voidaan erottaa kuvassa vielä toisistaan. Ja siis sitä lähempänä toisistaan olevia kohteita ei voi kuvassa erottaa toisistaan, vaan ne näkyvät yhtenä valoläiskänä.
Tämä tarkkuuden raja tunnetaan nimellä Rayleigh’n kriteeri, ja se sanoo, että sellaiset kohteet voidaan vielä erottaa toisistaan, joiden suuntaero $\theta$ on likimain
$$ \theta \approx 1.22 \frac{\lambda}{D},$$
missä $\lambda$ on aallonpituus, jolla kohdetta tarkastellaan, ja $D$ on edelleen aukon koko. Aallonpituuden merkitys on oleellisesti se valokuvauksessa, että se on pisin aallonpituus, jolla kohdetta kuvataan. Eli useimmiten punaisen valon aallonpituus.
Tämä sama raja pätee ihan yhtä lailla silloin, kun katsotaan kaukoputkella, otetaan valokuvaa, tai vaikka katsotaan paljaalla silmällä. Kun usein ajatellaan, että kaukoputkessa suurennus on tärkeä, niin kuitenkin aukon koko ratkaisee tarkkuuden. Siksi tähtiharrastajat usein pyrkivät käyttämään mahdollisimman suurta kaukoputken aukon kokoa – se mahdollistaa parhaan tarkkuuden. Ja sama tarkkuuskriteeri pätee myös valokuvaukseen. Aukon koko määrää sen, miten hyvään tarkkuuteen voidaan päästä parhaassa tapauksessa.
Ideaalisessa tapauksessa käy siis niin, että pienentämällä aukkolukua, objektiivin läpi tuleva valo pistemäisestä lähteestä kuvautuu pienemmälle alueelle. Eli aukkoluvun pienentämisestä on siis tuplahyöty kuvan ottamisessa: Isompi aukko kerää enemmän valoa, ja kerätty valo yhdestä kohteen pisteestä pakkautuu pienemmälle alueelle. Ja jos kuvataan tähtiä, niin yhdestä tähdestä tuleva valo jakaantuu harvemmalle pikselijoukolle.
Periaatteessa siis näin, mutta todellisuus on hiukan toisenlainen.
Todellinen aukko ja näennäinen aukko
Miten sitten aukko toimii oikeassa objektiivissa, joka ei ole yksittäinen linssi? Otanpa taas OpTaliX-ohjelmasta löytyvän esimerkkiobjektiivin tarkasteluun. Tällä kertaa kyseessä on 50 mm polttovälillä oleva linssi, jonka aukkoluku on maksimissaan $f/2.5$. Objektiivin rakenne on esitetty kuvassa 4.
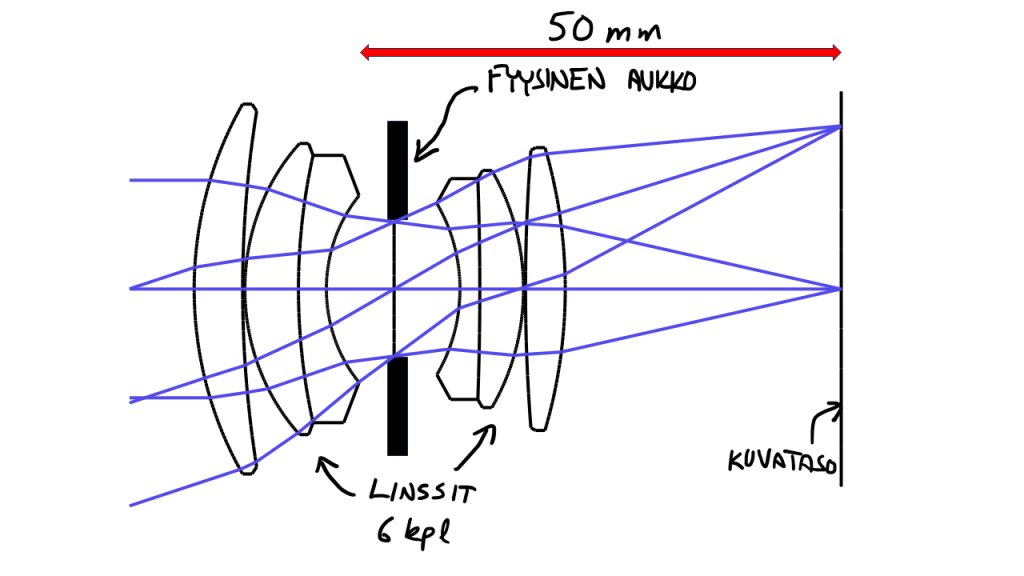
Kyseinen objektiivi koostuu kuudesta linssistä, jotka ovat neljää eri materiaalia. Kaikki linssit ovat pallopintaisia muodoltaan. Tästä tarpeesta käyttää useaa linssiä ja eri materiaaleja kirjoittanen sitten joskus oman juttunsa. Tällaisen suunnittelu kun ei ole mikään yksinkertainen tehtävä.
Objektiivin fyysisen aukon paikan olen merkinnyt kuvaan. Tämä on siis todellinen aukko, joka on toteutettu todellisissa linsseissä kuva 5 tyyppisellä systeemillä objektiivin sisällä.

Kuvan komponentin olen purkanut yhdestä rikkomastani objektiivista. Sen rakenteen keskellä näkyy viisikulmainen aukko. Sen reunat ovat itse asiassa lehdykkäisiä, joita pystyy liikuttamaan siten, että aukon koko joko pienenee tai suurenee. Suurimmillaan aukko voi olla mustia lehdykkäisiä ympäröivän kuparin värisen osan reiän suuruinen. Pienimmillään se voi olla hyvinkin pieni.
Tämä aukko on peräisin kamerasta, jossa aukon koko voidaan määrittään kameran asetuksista. Silloin se tarkoittaa sitä, että säädettävä aukko on itse asiassa laite, jossa on mukana sekä mekaniikkaa mahdollistamassa koon säätämisen, että elektroniikkaa, joka ohjaa sitä mekaniikkaa.
Tämä onkin hyvin tyypillistä optiikassa: Kun suunnitellaan optista laitetta – vaikka objektiivia – niin optiikan lisäksi usein mukaan tulee elektroniikkaa ja ja mekaniikkaa. Ja näiden osuus on osattava huomioida. Esimerkiksi objektiivin tapauksessa se tarkoittaa käytännössä sitä, että kun sinne sisään laitetaan säädettävä aukko, niin se vaatii jonkin verran tilaa, joka sille on varattava. Muuten laitetta ei voida oikeasti valmistaa ja kokoonpanna!
Tämä fyysisen aukon koko ei kuitenkaan ole ihan sama asia kuin aukkoluvussa käytetty aukon koko. Tätä olen hahmotellut kuvassa 6.
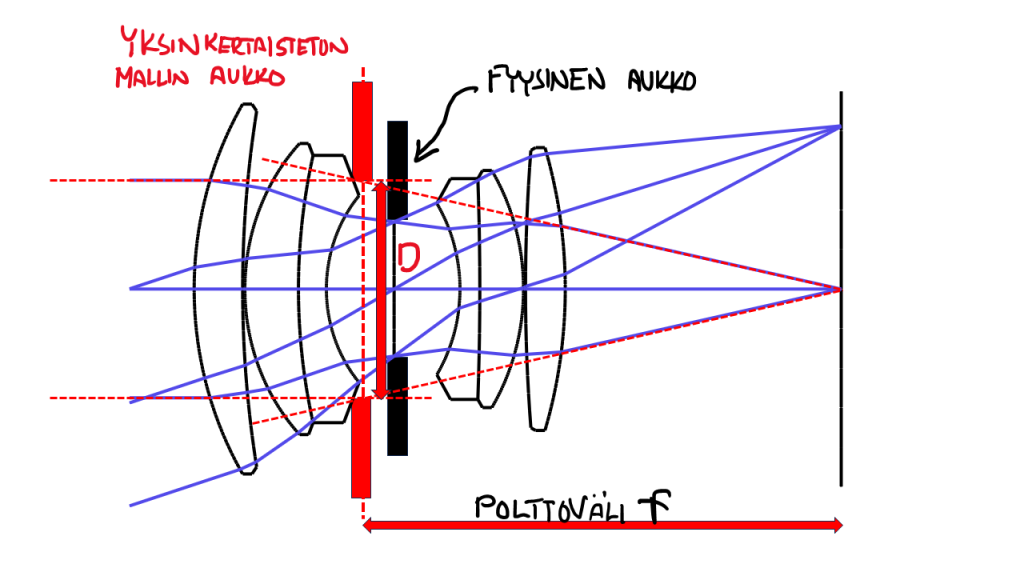
Kuten jo juttusarjan ensimmäisessä osassa käsittelin, objektiviille voidaan aina määrittää sen polttoväli, vaikka se koostuu useasta linssistä. Oleellisesti näin, kun olen kuvaan piirtänyt. Olen piirtänyt punaisella katkoviivalla suoraan linssille tulevan geometrisen säteen jatkeen. Ja sitten toisen vastaavan, joka tulee kuvatason fokuksesta pitkin sinne tulevaa viimeistä säteen pätkää. Ja polttoväli on matka näiden katkoviivojen risteyksestä kuvatasoon. Ja valon ”näkemän” aukon koon olen merkinnyt noilla punaisilla palkeilla.
Eli jos korvaisin siinä yksinkertaisimmassa mallissa tämän objektiivin yhdellä linssillä, niin tästä tulee sen polttoväli (joka on se 50 mm) ja aukon koko on tuo punaisten palkkien määräämä aukko, joka on nyt 50 mm / 2.5 = 20 mm, vaikka sen todellisen, fyysisen aukkokomponentin reiän koko on hiukan eri.
Ideaalinen kuva vs todellinen
Kuten edellä totesin, ideaalinen pistemäisen kohteen kuva saadaan Airyn kuviosta. Ja kuten arvata saattaa, todellisuus on toisenlainen.
Simuloin tätä kyseessä olevaa objektiivia. Käytin ensimmäisessä osassa ollutta yksinkertaista matematiikkaa, ja laskin, miten laajan kuva-alan tällainen objektiivi kattaisi kamerassani, joka on Canon EOS M50 mark ii. Siis sama, jota käytin osassa 2 kun analysoin linssiä. Sain, että kuva-ala on sellainen, että kennon nurkka vastaa noin 14.5 asteen kulmaa suhteessa keskipisteen kuvaamaan suuntaan. Joten laskin, millaiset kuvio muodostuvat sädekimpuista, jotka vastaavat kulmia 0, 5, 10 ja 15 astetta.
OpTaliX hoitaa tämän simuloinnin puolestani. Käytin kolmea eri valon aallonpituutta, ja kutakin vastasi aina joukko säteitä. Näiden osumapisteet olen esittänyt neljänä eri pistejoukkona kuvassa 7.
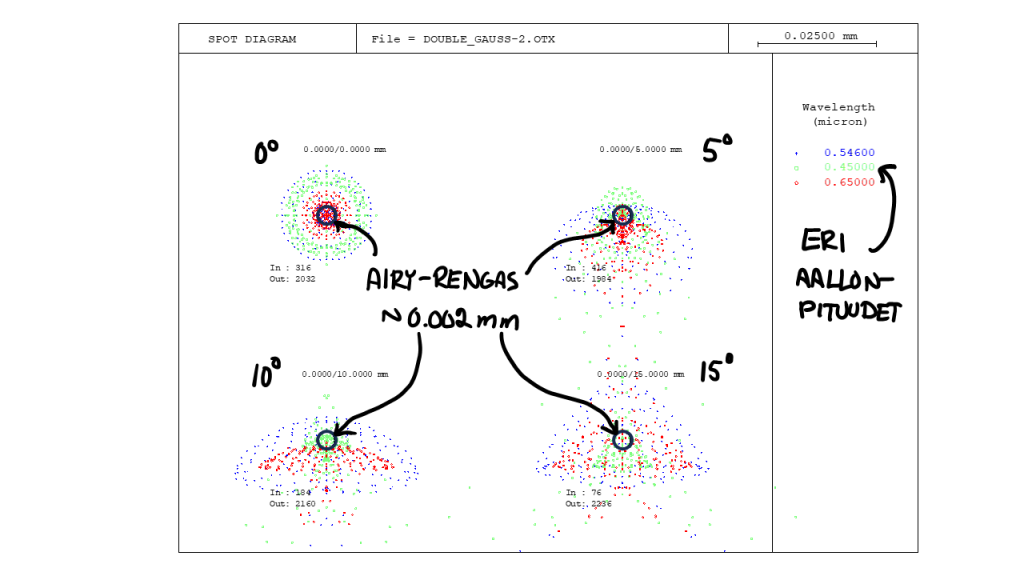
Kuhunkin kuvioon on merkitty myös aiemmin mainittu Airy-rengas. Eli se, minkä kokoinen olisi ideaalinen pisteen kuva. Tämä saavutetaan silloin, jos jokainen objektiivin läpi kulkenut säde osuisi täsmälleen kuvion keskipisteeseen.
Laskin, että pisimmälle lasketulle valon aallonpituudelle kyseinen Airy-rengas olisi kooltaan noin 0.002 millimetriä. Eli jos objektiivi olisi ideaalinen, niin tähteä kuvatessani yhden tähden kaikki valo osuisi yhden kameran pikselin alueelle, koska tuon kameran pikselit ovat 0.0037 millimetriä x 0.0037 millimetriä.
Mutta säteet eivät osu kaikki kuvion keskipisteeseen. Eivät edes kaikki sen renkaan sisälle. Se tarkoittaa sitä, että todellinen tähden kuva olisi jotain muuta. Käytännössä se olisi läpimitaltaan suunnilleen tuon pistejoukon läpimitta + Airy-renkaan halkaisija. Ja tässä tapauksessa siis näyttäisi joka keskellä kuvaa tuo todellinen pisteen kuva olevan noin 6x paras mahdollinen teoreettinen tarkkuus.
Mikä merkitys sitten on tuolla teoreettisella tarkkuudella, jos sitä ei tässä saavuteta? Sen suurin merkitys on siinä, että se kertoo objektiivin suunnittelijalle, että tämä on se, mihin kannattaa pyrkiä. Ja joissain tapauksissa siihen voidaan myös päästä, jolloin oltaessa sillä rajalla tarkkuudessa tiedetään, että ei kannata enää yrittää käyttää liikaa aikaa ja energiaa parantamiseen, koska todellisuudessa tarkkuus ei enää parane.
Toisaalta kun tiedetään, mikä on paras mahdollinen tarkkuus, johon voidaan päästä, voidaan objektiivin laatua verrata tähän ideaaliseen. Saadaan tavallaan mittari sille, miten hyvää laatua on saatu aikaan.
Ja kolmanneksi vielä kannattaa huomata, että tuota pienintä ideaalista kuvapisteen tarkkuutta kannatta hyödyntää sen kameran kuvakennon suunnittelussa. Ei kannata juurikaan tehdä pienempiä pikseleitä, kuin mitä on paras realistinen tarkkuus. ”Liian pienet” pikselit kun aiheuttavat monenlaisia haasteita: tähtiä kuvatessa yhden tähden valo jakautuu monelle pikselille, jolloin valon määrä yhdessä pikselissä on pienempi ja tarvitaan pitempiä valotusaikoja. Ja pienemmissä pikseleissä tulee enemmän kohinaa, joka sotkee kuvaa. Näitä kuvan tallentamiseen liittyviä asioita olen ajatellut kertoa sitten joskus myöhemmin.
Tässä tapauksessa siis kuusi linssiä ei tuota ideaalista tarkkuutta kyseisellä $f/2.5$ aukkoluvulla. Syynä on oleellisesti se, että tällä aukkoluvulla valonsäteiden kulkusuuntaa joutuu muuttamaan aika paljon linsseillä. Ja vielä niin, että valoa myös tulee aika erilaisissa kulmissa, joita kaikkia pitäisi hallita samoilla linsseillä. Ja kaiken lisäksi tässä tapauksessa linssit ovat pallopintaisia, joka rajoittaa aika paljon sitä, mitä voi tehdä.
Objektiivin laatua voisi kyllä yrittää parantaa sillä, että lisäisi linssien lukumäärää, ja optimoisi rakennetta sen jälkeen uudelleen. Tämäkään ei ole mitenkään automaattinen tie hyvään lopputulokseen. Systeemi tulee silloin monimutkaisemmaksi, painavammaksi ja kalliimmaksi, eikä kuitenkaan kuvanlaatu välttämättä merkittävästi parane.
Mutta aukon koon muuttaminen itse asiassa vaikuttaa kuvan laatuun. Vaikka teoreettinen, paras saavutettavissa oleva tarkkuus heikkenee aukkoa pienennettäessä, niin isoilla aukoilla tapahtuu yleensä päin vastoin todellisessa objektiivissa. Syynä on se, että aukon pienentäminen pienentää samalla niitä suurimpia kulmia, joihin valonsäteitä pitää kääntää. Ja tämä vähentää yleensä kuvausvirheitä.
Laskin, miten aukon pienentäminen arvoihin $f/4$ ja $f/8$ vaikuttaa tässä objektiivissa; tulos näkyy kuvassa 8.
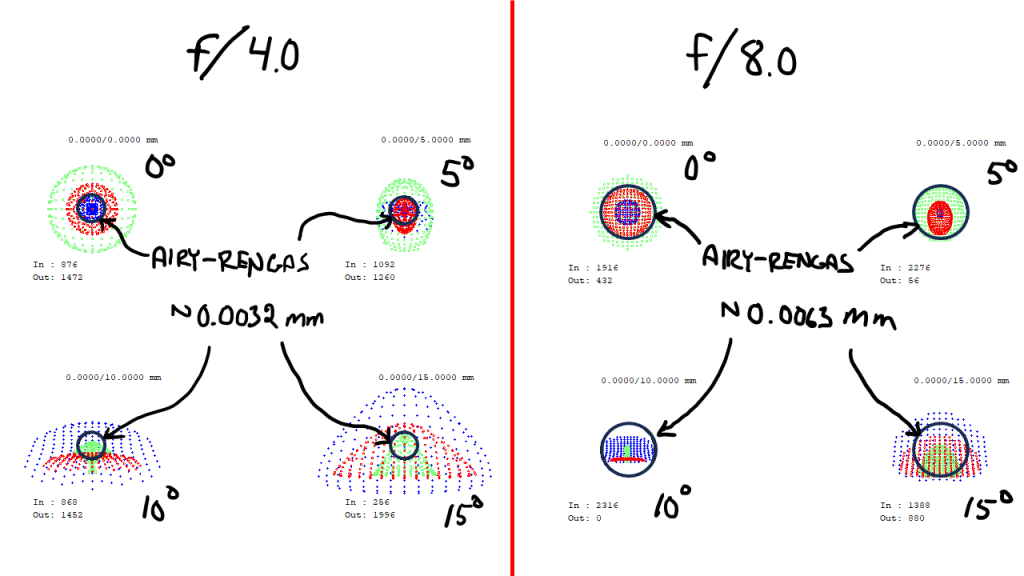
Vaikka kuviin piirretty Airy-rengas suurenee, eli teoreettinen paras mahdollinen tarkkuus heikkenee, niin säteet osuvat pienemmälle alalle kuvatasossa. Ja siis todellinen objektiivin tarkkuus on itse asiassa parempi näillä aukon arvoilla kuin aiemmalla $f/2.5$. Ja tämä on itse asiassa normaalia objektiiveilla: Paras todellinen tarkkuus saavutetaan usein aukon arvoilla välillä $f/4 – f/5.6$. Sen jälkeen aukko alkaa olla jo niin pieni, että on helppo päästä teoreettisen rajan lähelle, jolloin aukon pienentäminen heikentää tarkkuutta Airy-renkaan kasvaessa. Tätä tarkastelen hiukan lisää myöhemmässä artikkelissa, joka käsittelee objektiivien suunnittelua ja kuvan laatua tarkemmin.
Syvyysterävyys
Yksi käytännössä hyvin näkyvä aukon vaikutus on kuvan syvyysterävyys. Kuten ensimmäisessä osassa tarkastelin ohuen linssin kuvausyhtälön avulla, kuva on geometrisesti analysoituna tarkka vain yhdessä tasossa. Jolloin jossain toisessa tasossa oleva kohde ei ole enää täydellisesti tarkennettu. Tätä esittää kuva 9.
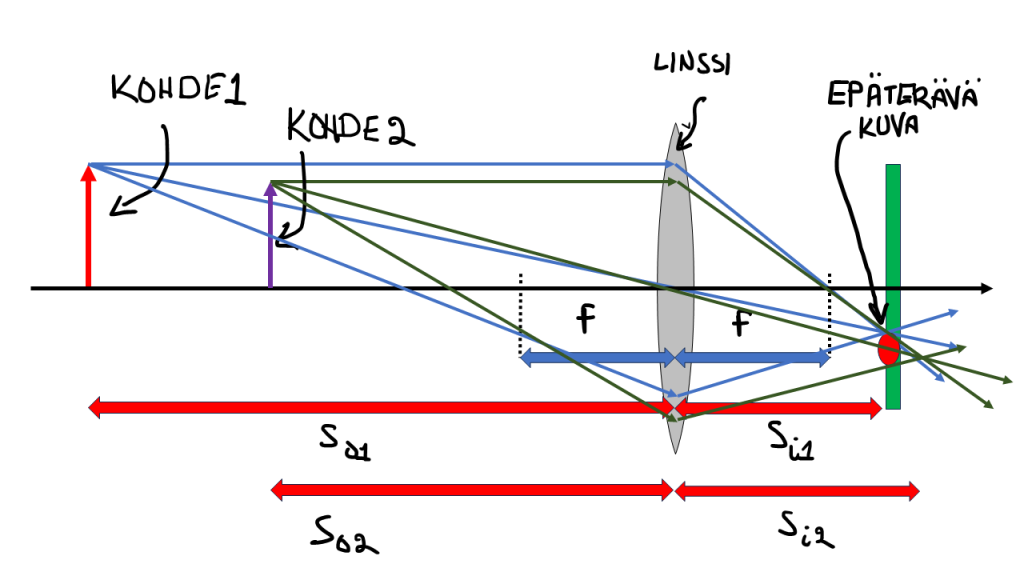
Kun kuvassa oleva kohde 1 on tarkka kuvatasossa – siis kameran kennolla – niin kohteen 2 kuva muodostuukin eri etäisyydelle. Tämän esimerkkikuvan tapauksessa, kohteen 2 kuva olisi terävä hiukan kauempana. Käyttäen ohuen linssin kuvausyhtälöä ja hiukan geometriaa, voi analysoida sitä, kuinka suurelle alueelle osuvat kohteesta 2 tulevat säteet. Tätä esittää kuvassa tuo punainen soikio. Ja helposti näkee, että tuon soikion koko kasvaa, kun linssin aukon kokoa kasvatetaan. Ja myös sen, että soikio on toisaalta sitä pienempi, mitä lähempänä kohde 2 on kohdetta 1. Tätä kutsutaan syvyysterävyydeksi.
Tätä olen konkreettisesti demonstroinut kuvassa 10. Otin naulajonosta kuvan käyttäen polttovälin 50 mm objektiivia, jonka suurin aukko on $f/1.4$. Otin kuvasarjan eri aukon arvoilla siten, että kaikissa kuvissa kamera on tarkennettu keskimmäiseen naulaan. Nauloista keskimmäinen oli noin 75 cm päässä kamerasta, ja naulojen välit olivat 5 cm.

Kuvasta näkyy hyvin, miten suurella aukolla (pieni aukkoluku) ainoastaan keskimmäinen naula näkyy terävänä. Ja aukkoa pienennettäessä syvyysterävyys paranee. Syvyysterävyys tai taustan häivyttäminen sen avulla ovat valokuvauksessa hyvin usein käytettyjä tehokeinoja. Tässä yhteydessä kannattaa muistaa, että pienempi aukko tarkoittaa vähemmän valoa. Jolloin aukkoluvun kasvattaminen vaatii samalla valotusajan pidentämisen, ellei halua kuvan muuttuvan pimeämmäksi. Mutta tästä yhteydestä kerron myöhemmin toisessa artikkelissa.
Miltä aukko näyttää ulospäin?
Aiemmin jo käsittelin sitä, että miltä aukko näyttää valon kannalta. Otanpa vielä käsittelyyn sen, miltä se näyttää ulospäin. Toki tämä on pitkälti samaa, kuin miltä se näyttää valon kannalta, koska mehän katsomme sitä valoa.
Kuvassa 11 on 20 mm laajakulmaisen objektiivin rakenne, lähteenä jälleen OpTaliXin kirjasto. Tätä samaa käsittelin jo sarjan ensimmäisessä artikkelissa.
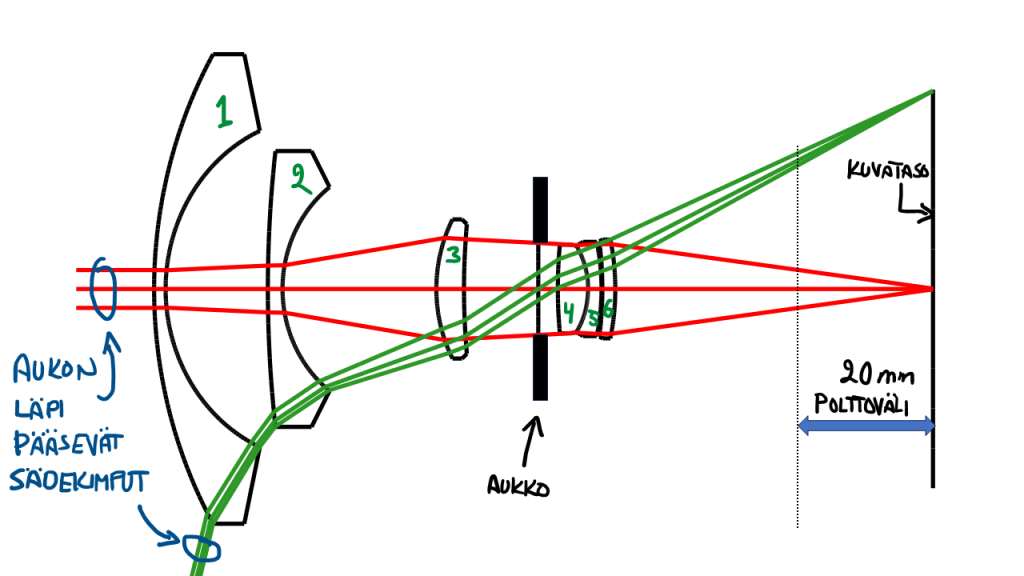
Kuvaan olen piirtänyt valonsäteitä, jotka tulevat kahdesta eri suunnasta siten, että näistä suunnista on mukana sellaisia, jotka pääsevät kuvatasolle asti. Ja ensimmäinen huomio on se, että kumpikin sädekimppu on reilusti pienempi kuin ensimmäisen linssin läpimitta. Ja tämä on hyvin tyypillistä laajakulmaisille objektiiveille. Eikä tämä itse asiassa ole mikään paha asia: Vaikka se tarkoittaa sitä, että linssit ovat suurempia (ja siten myös kalliimpia) kuin sädekimput, niin eri osiin linssiä osuminen antaa hiukan enemmän vapautta linssien suunnitteluun.
Tämä pieni kimppu suhteessa etummaisen linssin kokoon luonnollisesti tarkoittaa sitä, että aukko näyttä aika pieneltä suhteessa linssiin. Ja tätä demonstroin sitten yhdellä omistamallani laajakulmaisella 12 mm, $f/2$-aukkoisella Samyangin objektiivilla. Objektiivi näkyy kuvassa 12.

Koska polttoväli on 12 mm, ja suurin aukkoarvo on $f/2$, niin tällöin suurin valon näkemä aukon koko on 6 mm. Ja se on siis paljon vähemmän kuin etummaisen linssin läpimitta, joka on tällä objektiivilla noin 37 mm.
Kuvassa 13 olen sitten ottanut sellaiset valokuvat, joissa aukko näkyy edestä päin katsottuna. Otin kuvat siten, että laitoin objektiivin taakse kännykän, jossa näyttö oli valkoinen. Vasemmanpuoleisessa kuvassa näkyy aukko kuvattuna suunnilleen suoraan edestä. Oikeanpuoleisessa puolestaan aina vinosta, jolloin valo ei näytä tulevan linssin keskeltä, vaan lähempää etureunaa. Ja tämä siis vastaa nyt samaa, mikä näkyy noiden vihreiden säteiden kohdalla kuvassa 11.

Samoin otin myös kuvan aukosta kameran kennon suunnasta katsottuna, ja se on kuvassa 14. Täältä päin katsottuna aukko näkyy hiukan erilaisena. Ja itse asiassa tältä puolelta katsottuna näkyy hyvin myös kyseisen objektiivin aukon muoto, joka on hiukan pyöristynyt kuusikulmio.

Tämä aukon muoto sitten vielä lisäksi vaikuttaa siihen, miltä kuva näyttää silloin, kun tarkkuus on paras mahdollinen tai kun kohteena on pistemäinen valonlähde, joka on syvyysterävyysalueen ulkopuolella. Ensimmäisessä tapauksessa kyse on diffraktiosta; se saa Hubble-teleskoopinkin kuvissa kirkkaat tähdet näyttämään risteiltä. Sen tapauksessa aukon keskellä on este, jossa on ristikkäiset ripustustuet, jolloin diffraktiokuvio on ristimäinen. Jälkimmäisessä tapauksessa on sitten kyse Bokeh-efektistä, joka antaa epäteräville kohteille jonkinlaisen muodon.
Mutta nämä jääköön jo tämän tarinan ulkopuolelle, vaikka niissä oma kiinnostavuutensa on.

