Valokuvauksen optiikka – Osa 2

Linssit

Tämän sarjan ensimmäisessä jutussa käsittelin kameran objektiiveja yksinkertaisimmalla mallilla, joka on yksi ainoa linssi. Tässä toisessa osassa tarkastelen sitten linssejä, jolloin selviää myös, miksi yksi linssi ei kuitenkaan riitä kunnollisen objektiivin toteuttamiseen.

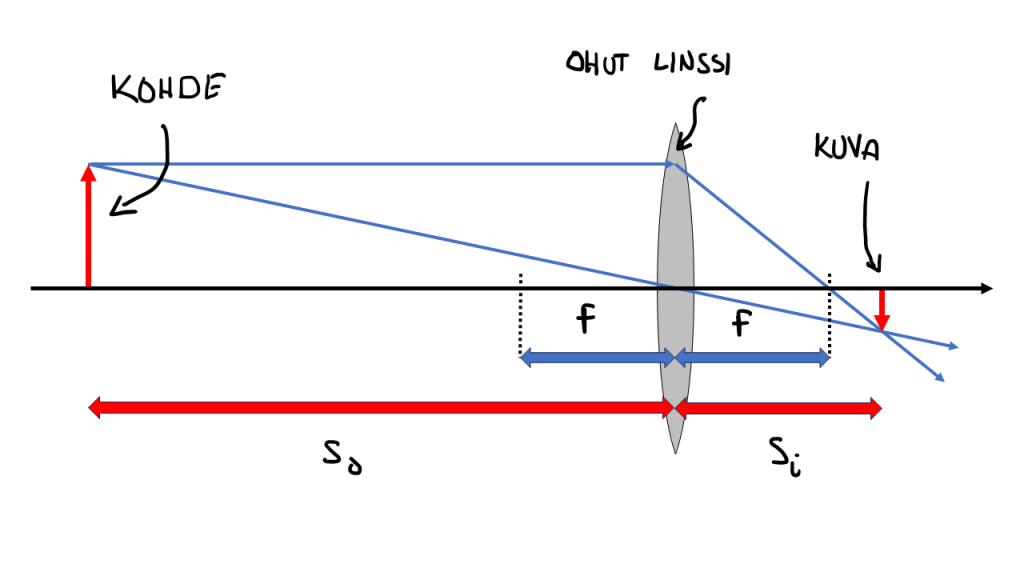
Kuvassa 1 on yhden linssin kuvaussysteemi. Periaatteessa siis tällainen voisi olla mahdollinen kameran objektiivina. Mutta lopputulos on sangen huono, jos ostaisimme linssin, ja rakentaisimme tällaisen kameraan. Lähdetään tarkastelemaan, että miksi näin käy.

Millainen on linssi?

Linssi itsessään on hyvin yksinkertainen kapistus. Se on vain palanen riittävän hyvin valoa läpäisevää materiaalia, jonka avulla muutetaan valon kulkusuuntaa. Hyvin usein etenkin järjestelmäkameran objektiiveissa linssit ovat erilaisia lasimateriaaleja. Ja vieläpä niin, että saman objektiivin eri linssit ovat eri materiaalia. Ja syyn tähän kerron tarkemmin hiukan myöhemmin.

Yleensä linssin muoto on sellainen, että sen etu- ja takapinta ovat pallopinnan muotoa, kuten olen hahmotellut kuvaan 2. Pinnoilla on kaarevuussäteet $R_1$ ja $R_2$, ja linssin materiaalilla on materiaalille ominainen taitekerroin $n$. Nimensä mukaisesti tämä vaikuttaa valon taittumiseen, kuten kohta kerron tarkemmin.

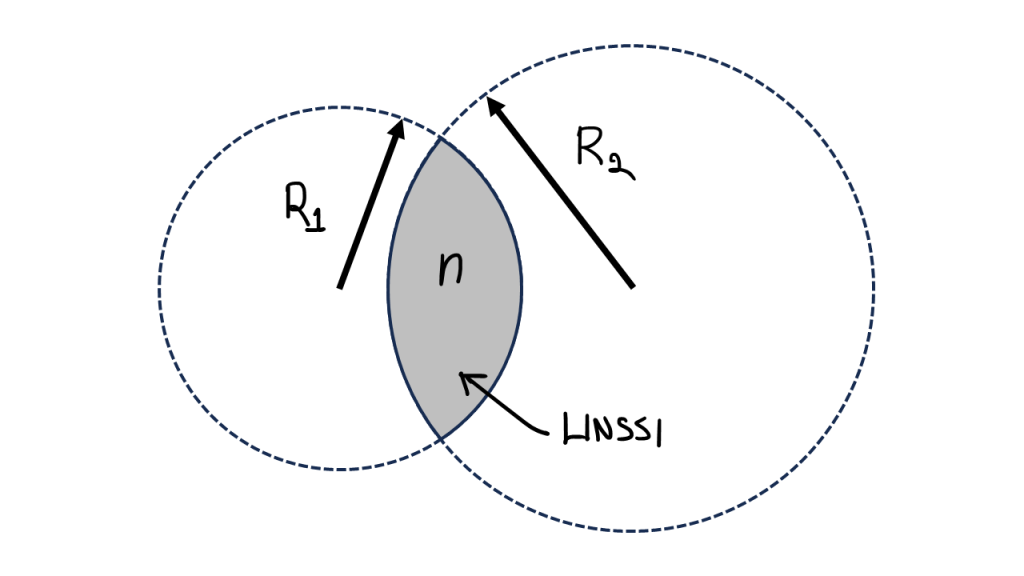
Syy sille, miksi linssin pinnat ovat usein pallopinnan muotoisia on se, miten linssin saa valmistettua. Lasista tehty linssi on sangen yksinkertainen valmistaa lasia hiomalla ja kiillottamalla, ja sen pinnan muoto on helposti varmennettavissa, mikäli pinta on pallopinnan muotoa.

Jos kiinnostaa, miten linssejä ja linssisysteemejä valmistetaan, niin voit katsoa sen vaikka tästä:

How camera lenses are made (youtube.com)

Kuvassa näemme, että linssin hiominen ja kiillottaminen tapahtuvat suurelta osin automaattisesti. Tämä on mahdollista erityisesti silloin, kun linssin pinta on pallonmuotoinen.

Muunkin muotoisia pintoja voi valmistaa. Mutta niiden osalta valmistusprosessi on työläämpi, samoin pinnan mittaaminen. Siksi ne ovat yleensä paljon kalliimpia valmistaa. Ja vaikka niiden avulla voidaankin joskus hyvinkin tehokkaasti korjata myöhemmin esittelemiäni kuvauksen virheitä, ovat objektiivin linssit suurimmalta osin pallopintaisia kustannussyistä. Aika usein objektiivin linsseistä 1-2 on muodoltaan muita kuin pallopintaisia, kun objektiivin linssimäärä on yhteensä tyypillisesti noin kymmenen.

Kännykän kameroiden linsseissä käytetään sitten useammin ei-pallopintaisia linssejä. Kännykän kamerat ovat paljon pienempiä, jolloin linssien valmistus voidaan tehdä toisenlaisilla menetelmillä, jotka mahdollistavat monimutkaisempien pintojen valmistamisen suhteellisen helposti. Mutta näihin en nyt tarkemmin puutu.

Mitä linssi sitten tekee valolle? Oleellisesti se siis muuttaa valon kulkusuuntaa siten, että se esimerkiksi fokusoi valon ja muodostaa kuvan kohteesta kameran tapauksessa. Tätä voidaan mallintaa itse asiassa sangen helposti kuvan 3 mukaisesti.

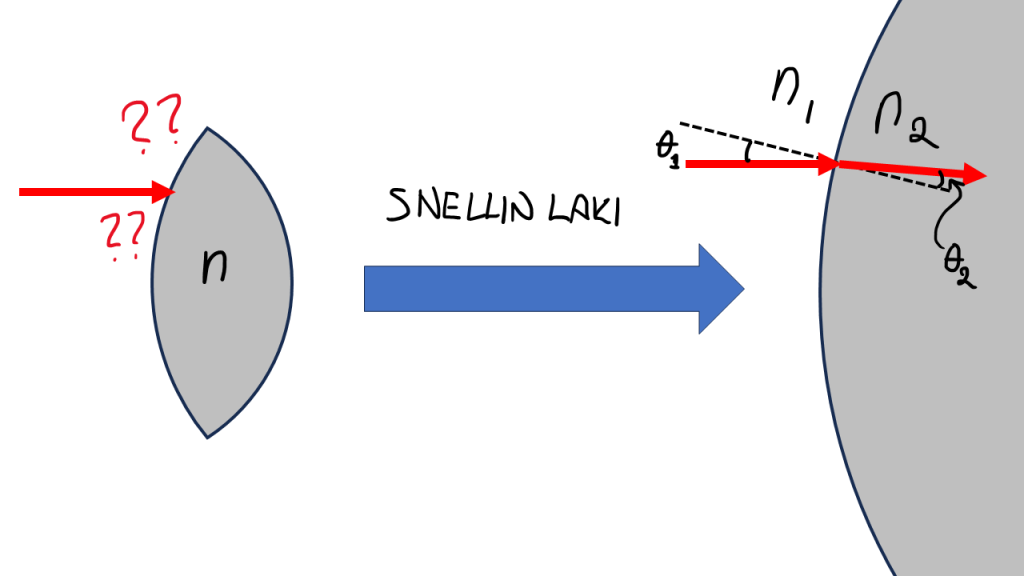
Kuten aiemmin totesin, kullakin materiaalilla on sille ominainen taitekerroin; sitä merkitään usein kirjaimella $n$. Pohjimmiltaan se kuvaa sitä, millä nopeudella valo etenee materiaalin sisällä. Ja tällä on sitten se seuraus, että valon tullessa vaikka ilman ja kyseisen materiaalin rajapinnalle, valon kulkusuunta muuttuu niin sanotun Snellin lain mukaisesti.

Snellin laissa on kyse tästä: Ajatellaan, että voimme kuvata valon osumista kahden eri materiaalin rajapinnalle – vaikka ilman ja lasin – käyttämällä geometristä sädettä niin kuin tein jo kuvassa 1. Eri materiaaleilla on eri taitekertoimet; merkitään niitä vaikka siten, että etupuolella taitekerroin on $n_1$ ja takapuolella se on $n_2$. Kun säde osuu pinnalle kulmassa $\theta_1$, niin tällöin säde taittuu kulmaan $\theta_2$ siten, että

$$ n_1 \sin(\theta_1) = n_2 \sin(\theta_2) $$

Ja tämä on nyt Snellin laki. Täysin tarkka tämä ei ole kaikelle valolle, mutta usein riittävän hyvä linssille, jos linssin koko on tarpeeksi iso, ja sen pinta on riittävän hyvin muotoiltu.

Tämän yhden ainoan yhtälön avulla voidaan sitten analysoida kokonaisia linssisysteemejä, kun lisänä vaan otetaan mukaan säteen suoraviivainen eteneminen materiaalin sisällä – jos vaan materiaali on riittävän tasalaatuista. Ja optiikan suunnittelu- ja analysointiohjelmat laskevat yleensä suuren joukon kohteesta tulevia valonsäteitä, ja määrittävät tämän lain avulla, mihin pisteeseen kuvatasoa nämä säteet osuvat.

Jo tässä vaiheessa otan sitten mukaan ensimmäisen linssin toimintaan vaikuttavan tekijän, ja se liittyy tuohon taitekertoimeen. Nimittäin se ei ole materiaalille yksi ainoa numero, vaan se riippuu valon aallonpituudesta. Tätä kutsutaan dispersioksi. Käytännössä lyhyille aallonpituuksille se on suurempi kuin pitemmille johtuen siitä, miten valo vuorovaikuttaa atomien elektronien kanssa. Jolloin käytännössä siis sininen valo taittuu voimakkaammin kuin vihreä tai punainen. Ja koska valokuvauksessa on mukana yleensä kaiken väristä valoa, niin voi arvata, että tämä tulee aiheuttamaan jotain haasteita.

Kuvassa 2 minulla oli piirrettynä yksinkertainen, pallopintainen linssi. Käyttämällä Snellin lakia, saadaan sitten yhteys tämän rakenteen ja linssin polttovälin välille. Tämä yhteys tunnetaan nimellä ”linssin tekijän yhtälö,” joka on hyvin yksinkertainen, jos voimme jättää huomiotta linssin todellisen paksuuden ja oletamme, että linssiä ympäröi ilma:

$$ \frac{1}{f} = (n-1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right)$$

missä siis $f$ on linssin polttoväli, $n$ on materiaalin taitekerroin, ja $R_1$ ja $R_2$ ovat pintojen kaarevuussäteet niin kuin piirsin kuvaan 2. Ja tämän avulla siis linssin tekijä voi toteuttaa linssin, jolla on haluttu polttoväli.

Tästä voi jo ennen sen suurempaa analyysia havaita kaksi asiaa: (1) koska taitekerroin riippuu valon aallonpituudesta, yksi linssi ei voi toimia oikein kaikille aallonpituuksille. Ja se on huono asia. (2) Tämä yhtälö ei itse asiassa määrää kaarevuussäteitä, vaan niiden keskinäisen suhteen. Ja se on hyvä asia, koska muuttamalla näitä sopivasti, polttoväli ei muutu, mutta muutos vaikuttaa linssin kuvausvirheisiin jonkin verran.

Yksi linssi = ei hyvä

Katsotaanpa sitten, miten hyvin yksi yksittäinen linssi sitten oikeasti voi toimia. Meillä on nyt työkalut siihen: Kun olen valinnut halutun objektiivin polttovälin, niin voin suunnitella linssin linssitekijän yhtälöllä. Teen siinä pari valintaa: ensinnäkin valitsen linssille lasin materiaaliksi BK7, joka on aika helposti saatavilla oleva materiaali linsseille. Toisekseen, valitsen sellaisen linssin, jonka molemmat puolet ovat kaarevuudeltaan samat; tällaista sanotaan kaksoiskuperaksi linssiksi.

Otan esimerkkipolttoväliksi 40 mm; tällainen olisi kamerallani Canon EOS M50 mark ii ihan hyvä polttoväli, jos haluaisin vaikka ottaa kuvia ihmisistä. Sen lisäksi valitsen linssin halkaisijaksi 16 mm, joka tarkoittaisi kameran objektiivina aukkoarvoa F/2.5. Ja tämähän olisi ihan jo kelvollinen objektiivi muotokuvien kuvaamiseen – jos siis toimisi hyvin.

Voin analysoida aika helposti tällaisen linssin. Se onnistuisi muutenkin kohtuullisesti. Kyse on vain Snellin lain soveltamisesta, ja sen laskemisesta, mihin säde osuu linssillä. Tämä jälkimmäinen on sama kuin suoran ja pallopinnan leikkauspisteiden laskeminen matematiikassa.

Mutta jos et osaa tai muista tämän laskemista, niin ei mitään huolta. Koska saatavilla on valmiita ohjelmia, niin käytän sellaista sen sijaan, että ryhtyisin itse noita kaavoja paperilla laskemaan tai edes valmiita kaavoja koodiksi kirjoittamaa.. Käytössäni on OpTaliX-niminen optiikan suunnittelu- ja analysointiohjelma.

Ja sen kirjastosta löytyy jopa valmiina linssi, joka vastaa noita parametrejäni. Parametrien syöttö ohjelmaan, ja kone laskee, miten suoraan edestä tuleva sädekimppu kulkee linssin läpi kameran sensorille. Tästä kone piirtää minulle kuvassa 4 näkyvän sädekimpun.

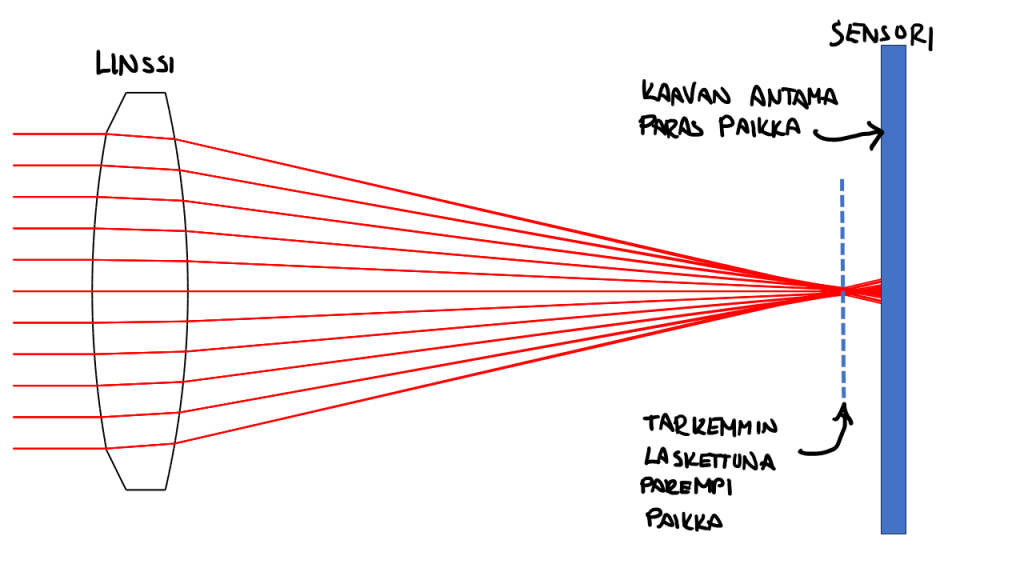
Jos heti näkyy, että ihan optimaalisesti tämä ei mennyt. Kaikki säteet eivät osu saman kohtaan, ja sensori ei näytä olevan edes sädekimpun kapeimmassa kohdassa. Syynä tähän on se, että suunnittelussa on käytetty approksimaatiota, joka ei huomioi sitä, miten erityisesti linssin reunoille osuvat säteet taittuvat. Linssin pallopintainen muoto aiheuttaa sen, että linssin reunalle osuvat säteet kääntyvät eri suuntaan kuin keskemmälle osuvien säteiden muodostama fokus.

Tätä kutsutaan palloaberraatioksi. Eli pallopintainen linssi ei ole optimaalinen edes suoraan edestä tulevalle valolle. Tämän korjaamiseen löytyy kyllä keinoja, mutta en käy niitä tässä artikkelissa käymään läpi. Tämä ei nimittäin kuitenkaan ole ainoa ongelmamme tässä systeemissä.

Hyvin helposti saan kuitenkin tuolla ohjelmalla nyt etsittyä sen kohdan, jossa sädekimppu on pienimmillään. Joka siis vastaa sitä, kun kamera tekee tarkennuksen. Ja on myös helppo piirtää säteiden osumakohdat kameran kennon tasossa. Olen tehnyt sen kuvassa 5 siten, että ne on laskettu viidessä eri tarkennuksen kohdassa, jossa keskimmäinen on tarkin. Siniset, vihreät ja punaiset merkit vastaavat kyseisen väristä valoa.

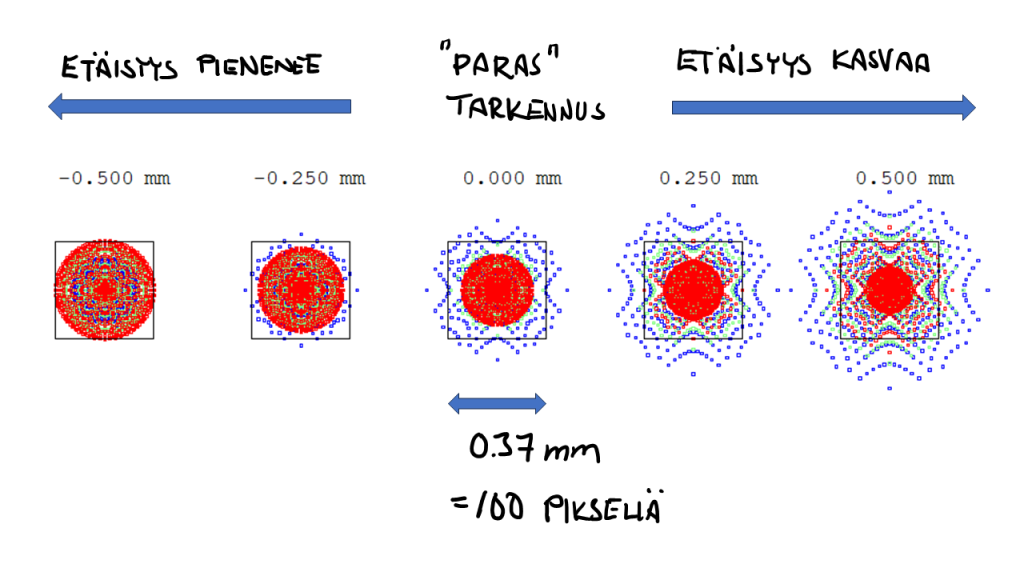
Ensimmäinen huomio on se, että eri värit muodostavat pienimmän pistejoukon eri etäisyyksillä linssistä. Siniset säteet fokusoituvat lähimpänä linssiä, ja punaiset kauempana, ja vihreät suunnilleen siinä, missä ollaan parhaassa tarkennuksessa, eli keskimmäisessä pistejoukossa. Tämä on suora seuraus siitä, että lasin taitekerroin riippuu valon aallonpituudesta. Ja tämä aiheuttaisi sitten erilaisia värivirheitä oikeassa kuvassa.

Vaikka pistejoukot näyttävät suhteellisen pieniltä, niin ei kannata antaa sen hämätä. Kuvan 5 pistejoukkoihin on piirretty neliöt, joiden koko on 0.37 millimetriä. Tuon kameran yhden pikselin koko on 0.0037 millimetriä kertaa 0.0037 millimetriä, eli neliöt vastaavat itse asiassa 100 x 100 pikselin aluetta kameran kennolla. Ja tämä tarkoittaa käytännössä sitä, että jos ottaisin tuolla kamerasysteemilläni nyt kuvan tähtitaivaasta, niin kukin yksittäinen tähti näyttäisi kuvassa läiskältä, jonka läpimitta on noin 100 pikseliä.

Ja se on paljon: jos noilla mitoilla onnistuisi tekemään optimaalisen kameran objektiivin, niin sen kuvaamana tähti näyttäisi suunnilleen yhden pikselin suuruiselta kennolla. Tämä pienin teoreettinen kuvapisteen koko riippuu siitä, mikä on linssin läpimitan ja polttovälin suhde – eli aukkoluku. Ja lisäksi tämä riippuu myös valon aallonpituudesta. Ja jos pääsisi ideaaliseen kuvautumiseen, niin kameralle tällaisella linssillä tallentuva kuva olisi aika lailla sillä tavalla pistemäinen, kuin mitä ne taivaalla meille näkyen ovat.

Toisin sanoen, edes suoraan edestä tulevalle valolle tuo objektiivi ei olisi edes keskinkertainen. Se olisi laadultaan suoraan sanottuna erittäin huono. Ja vielä huonommalta tilanne näyttää silloin, jos katsotaan, miten kameran kennon reunalla kuva näyttäisi.

Edellisessä artikkelissani kerroin, että on hyvin helppo laskea, mikä on kameran näkökenttä, kun objektiivin polttoväli ja kennon koko tiedetään. Tälle systeemilleni kuva-ala olisi sellainen, että aivan kennon nurkkaan osuvat säteet olisivat sellaiset, että valo tulisi noin 18 asteen kulmassa. Siispä lasken myös, miten valo käyttäytyy kulmilla 0, 8 ja 16 astetta, joista viimeinen on siis vähän pienempi kuin linssin suurin kuva-alan suunta. Ja lopputulos on kuvassa 6.

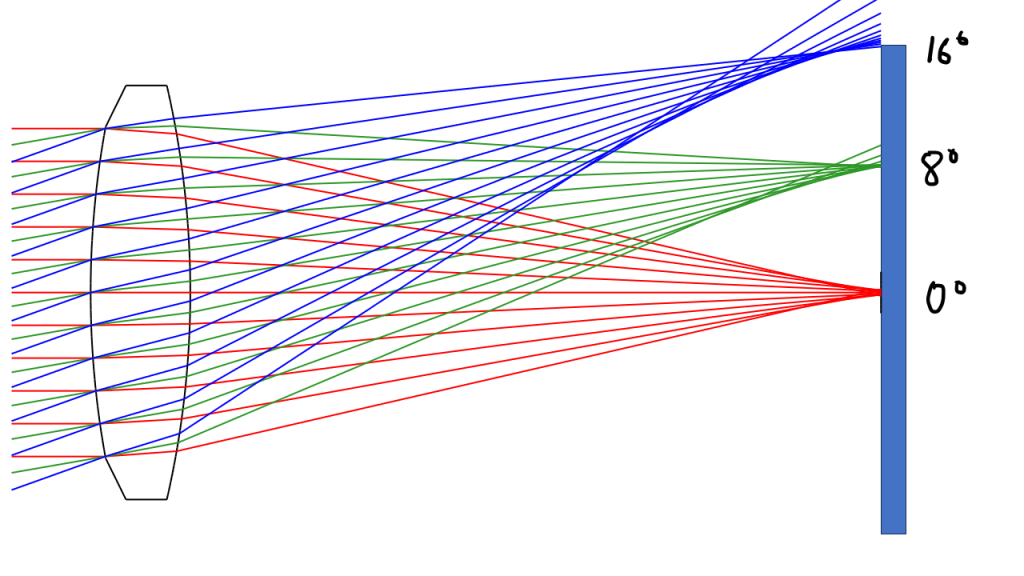
Kuvasta näkyy hyvin, miten kulman kasvattaminen saa aikaan sädekimpun fokusoitumisen heikkenemisen. Ja suurella kulmalla näyttää siltä, että lukuun ottamatta joitain reunimmaisia säteitä, myös tarkimman fokuksen kohta on eri etäisyydellä linssistä kuin linssin keskellä.

Näitä kuvausvirheitä eli aberraatioita on optiikassa paljon tutkittu ja kehitetty menetelmiä niiden korjaamiseen. Tämä on käytännössä sitä, jonka ratkaisemiseen kameran objektiiveja suunnitteleva sitten pitkälti paneutuu. Ja tämä kuvausvirheiden korjaaminen on sitä, mikä lopulta vaatii linssisysteemejä olemaan sangen monimutkaisia, jos hyvää kuvanlaatua halutaan.

Laskin myös näiden säteiden osumisen kennolla, joka on esitetty kuvassa 7. Siinä näkyy hyvin se, miten kuvan laatu heikkenee kulman kasvaessa.

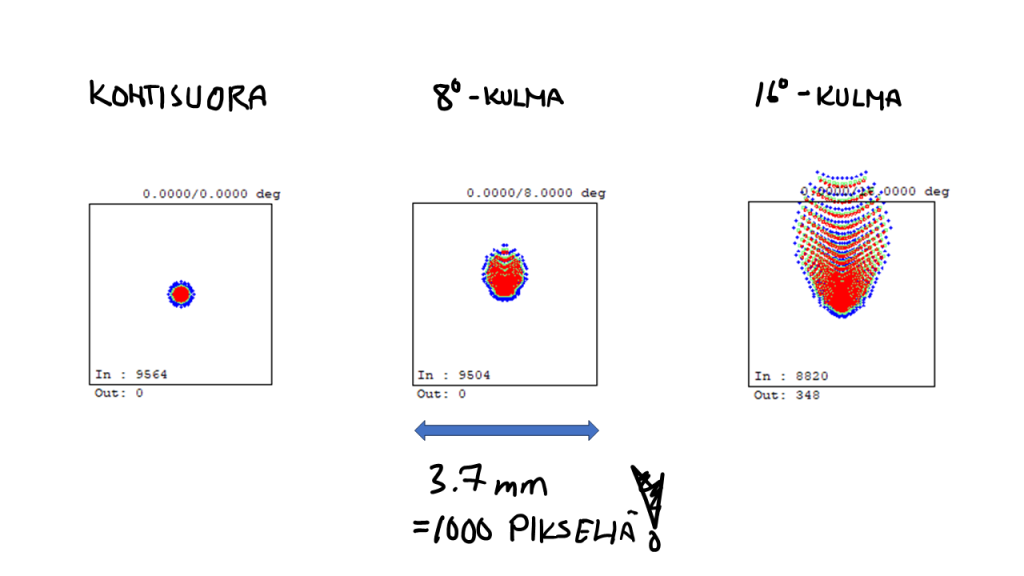
Kennon nurkassa kuvan laatu on jo erittäin huono: Tässä neliön koko on jo 1000 x 1000 pikseliä, joka on jo aika suuri osa kyseisestä 6000 x 4000 pikselin kennosta. Käytännössä tarkoittaa siis sitä, että tällainen objektiivi olisi lähinnä käyttökelvoton valokuvaukseen.

Tämä esimerkkini siis näyttää vahvasti siltä, että tällä yhden linssin systeemillä ei päästä hyvään – eikä edes tyydyttävään kuvanlaatuun. On nimittäin aika vähän mahdollisuuksia korjata tätä yksittäistä linssiä, jos halutaan säilyttää valmistuksen kannalta helppo pallopinta.

Pintojen kaarevuussäteitä ja linssin paksuutta voi koettaa muuttaa, mutta se ei paljon noita virheitä korjaa. Ainoa parannukseen oikeasti johtava keino olisi suurentaa linssin aukkolukua, eli pienentää linssin läpimittaa. Mutta kuten myöhemmin tulevassa toisessa artikkelissa aion kertoa, tämä tarkoittaa sitä, että valon määrä kennolle vähenee. Josta aiheutuu omat ongelmansa. Eikä tämä edes poista lopulta kaikkia kuvausvirheitä.

Siksipä todelliset objektiivit ovat sellaisia, joissa sitten on isompi määrä linssejä. Yksinkertaisimmissa puolenkymmentä; monimutkaisemmissa jopa parikymmentä. Ja tähän asiaan aion myös paneutua jossain myöhemmässä artikkelissa.

Yhteenvetona toteaisin: yhden linssin malli objektiiville on hyvä työkalu analysoinnissa. Mutta yksi yksittäinen linssi ei tuota hyvää kuvanlaatua.