Objektiivin polttoväli ja näkökenttä
Ajattelin aloittaa pienen juttusarjan valokuvauksen optiikasta. Koska tämä ei ole mikään opetuskanava, niin en aio käydä läpi kaikkea tieteellisen tarkasti. Yksi yhtälö tässä ensimmäisessä osassa esiintyy, mutta ei sen enempää. Mutta kyseessä onkin aika yksinkertainen ja käyttökelpoinen yhtälö.
Mikäli halua oppia enemmän optiikasta, niin vilkaise vaikka yliopistomme online-kurssit Valo ja Fotoniikkaa kaikille. Samoin internetistä löytyy paljon vapaasti luettavaa oppikirjamateriaalia optiikasta, esimerkiksi kirjasarjasta University Physics optiikan osuus.
Ajatuksenani on, että tämä artikkeli saa sitten jatko-osia, joissa käsittelen muita valokuvauksen optiikkaan liittyviä asioita. Kuten vaikka miksi objektiivit koostuvat useista linsseistä, miten kameran kenno toimii, tai mitä voimme sanoa kuvan laadusta.
Objektiivi ja sen yksinkertaistus
Todellinen kameran objektiivi on yleensä aika monimutkainen laite. Se koostuu useista lasilinsseistä, mekaniikasta, ja usein myös elektroniikasta. Kuvassa 1 on valokuva todellisesta kameran objektiivista, ja sen yksinkertaisimmasta toimintamallista.

Vaikka objektiivi on monimutkainen, niin yksinkertaisimmassa mallissa se korvataan vain yhdellä linssillä, jonka polttoväli on kyseisen objektiivin polttoväli. Lisäksi hyvin tärkeässä roolissa on myös linssin aukon koko, mutta siihen en vielä tässä ensimmäisessä osassa juurikaan puutu. Huomautan vaan, että aukon koko on eri asia kuin objektiivin linssin läpimitta.
Optiikan puolella ei riitä se, että otetaan vaan joku malli. Kyseisen mallille pitää olla joku perustelu, että miksi sitä voi käyttää. Sen lisäksi pitää myös ymmärtää, mitkä ovat sen kyseisen mallin käytön rajoitukset. Eli käytännössä: miten suuren virheen teemme eri tapauksissa, jos käytämme tätä kyseistä mallia.
Optiikassa voidaan itse asiassa aina muodostaa linssisysteemistä yksinkertaistettu malli, jossa monen linssin systeemi on korvattu yhdellä linssillä. Tämä yhteys on hahmotettu kuvaan 2. Siinä on yksi monen linssin avulla toteutettu laajakulmainen kameran objektiivi.

Objektiivin toiminta mallinnetaan hyvin usein geometrisinä säteinä, jotka mallintavat valon kulkemista linssisysteemin läpi. Kuvan tapauksessa punaisilla viivoilla on piirretty muutama säde, jotka tulevat kohtisuoraan edestä. Tämä mallintaa äärettömän kaukana olevan kuvattavan pisteen lähettämän valon kulkua linssisysteemin läpi.
Linssit ohjaavat näiden säteiden kulkua siten, että nämä yhdestä pisteestä tulevat säteet fokusoituvat lopulta kuvatasolle, jossa siis sijaitsee kameran kenno. Tämä linssisysteemi koostuu useammasta, eri materiaaleita ja eri muotoisilla linssipinnoilla toteutetuista linsseistä. Syy monimutkaisuuteen on se, että näin saadaan kyseiset säteet osumaan riittävän hyvin yhteen pisteeseen kuvatasolla. Eikä pelkästään näiden punaisten säteiden tapauksessa, vaan myös kaikkien muiden oikealla etäisyydellä olevien kohteen pisteiden lähettämät valonsäteet; kuten vaikka vihreällä piirretyt toisesta pisteestä tulevat.
Jossain toisessa kirjoituksessa tulen sitten tarkastelemaan tätä tarvittavaa monimutkaisempaa rakennetta. Lyhyesti sanottuna: yhdellä linssillä ei saavuteta riittävän hyvää kuvanlaatua.
Mutta joitain asioita voimme kyllä tarkastella tästä muodostetulla yhden linssin mallilla. Oleellisesti malli on sellainen linssi, jolla on kyseisen linssisysteemin yhdistetty polttoväli. Kuvassa 2 se on hahmoteltu seuraavasti: Yhdelle noista punaisista säteistä olen piirtänyt katkoviivalla jatkeen, joka kulkee alkuperäiseen suuntaan; varsinainen säteen kulku on yhtenäisellä punaisella viivalla. Kun sitten viimeisen linssi jälkeen tämä alkuperäisen suunnan katkoviiva ja oikea säteen yhtenäinen viiva leikkaavat (olen ympyröinyt punaisella sen leikkauspisteen), niin tähän kohtaan laitettu linssi vastaa tämän linssisysteemin toimintaa. Ja sen linssin polttovälin pitää olla tuon leikkauspisteen etäisyys kuvatasosta, jos se alkuperäinen kuvattavana oleva piste on äärettömän kaukana.
Tämä matka on siis tässä nimenomaisessa tapauksessa pitempi, kuin matka viimeisestä linssistä kuvatasoon. Tämä on hyvin tyypillistä etenkin vähänkin vanhemmille järjestelmäkameroiden objektiiveille: niillä kun pitää objektiivin ja kennon väliin mahtua kääntyvä peili, jolla mahdollisestaan etsimen käyttö. Esimerkiksi Canonin kameroissa tämä etäisyys objektiivin kiinnityksestä kameran kennoille on ollut peilikameroissa 55 mm. Ja kaikilla objektiiveilla siis pitää olla vähintään tämä matka tällöin viimeisestä linssistä kennolle, jos kyseessä on peilikameroissa toimiva objektiivi.
Ja tämä on yksi syy, miksi esimerkiksi kuvassa 1 oleva Irix-objektiivi on noin pitkä. Objektiivin linssisysteemi on pitänyt suunnitella sellaiseksi, että kyseinen takapolttoväli on riittävän iso. Ja toisekseen, riittävän hyvä kuvan laadun saavuttamiseksi objektiivin pitää todellisuudessa koostua useasta linssistä. Tuon Irix-objektiivin sisällä on 15 linssiä.
Tämä yksinkertaistettu objektiivin malli on approksimaatio. Se toimii sangen hyvin niille valonsäteille, jotka tulevat suunnilleen kohtisuoraan edestä linssille. Mutta esimerkiksi kuvassa 2 olevat vihreällä piirretyt säteet eivät enää ole mallinnettavissa oikein tuolla yhdellä linssillä, vaan tarvitaan tarkempi mallinnus. Joka sitten tehdään optiikan suunnitteluohjelmilla.
Lähdetään seuraavaksi tarkastelemaan hiukan mitä voimme sanoa objektiivin toiminnasta käyttäen tätä yhden linssin mallia.
Polttoväli ja kuvan muodostuminen
Kohteen kuvautumisen ohuesta linssistä voi laskea ohuen linssin yhtälöllä. Se ei ole tarkka analyysi kuvautumiselle, mutta silti monessa tilanteessa yksinkertaisuudessaan hyödyllinen. Ohuen linssin yhtälö kertoo oleellisesti sen, että mille etäisyydelle muodostuu kuva, kun käytetään yhtä linssiä kohteen kuvaamiseseen. Yhtälö menee näin:
$ \frac{1}{f} = \frac{1}{s_o} + \frac{1}{s_i}, $
missä $f$ on linssin polttoväli, $s_o$ on kohteen (objektin) etäisyys linssistä, ja $s_i$ on linssin kohteesta muodostaman kuvan etäisyys linssistä; katso kuva 3.
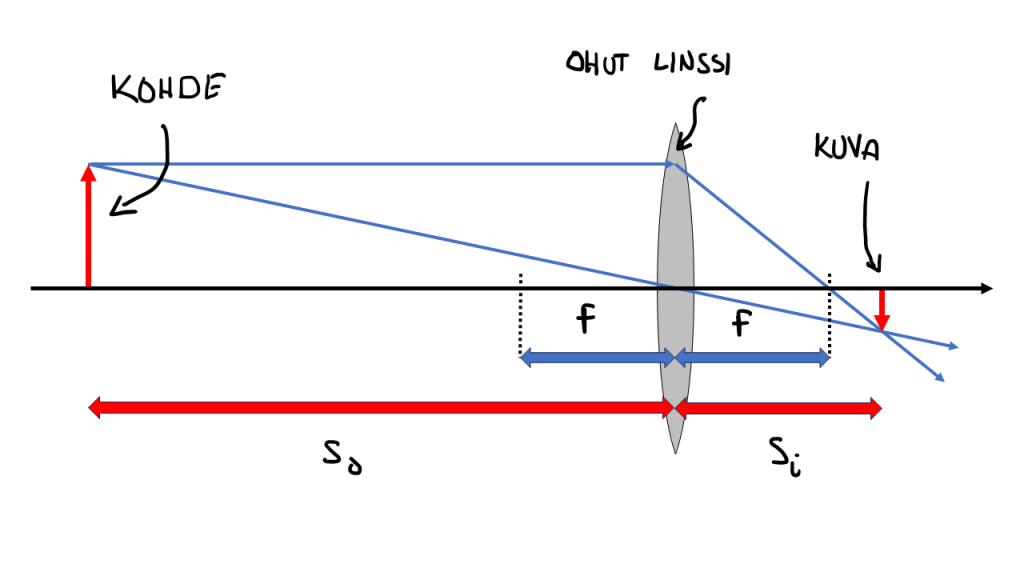
Toisin kuin ehkä voisi siis aluksi kuvitella, kuva ei kamerassa muodostu linssin polttovälin päähän linssistä – paitsi silloin, kun kuvattava kohde on äärettömän kaukana objektiivista – ja tämä tapaus on itse asiassa se, millä polttoväli määritellään. Normaalisti kuitenkin kohde on suhteellisen kaukana verrattuna polttoväliin $f$, jolloin käytännössä kuva muodostuu usein aika lähelle polttotasoa. Poikkeuksena makrokuvaus, jossa kohde lähelle objektiivia.
Tämä kuvan paikan riippuvuus kohteen etäisyydestä on se, jonka takia kameran objektiivi pitää tarkentaa aina sen mukaan, millä etäisyydellä kohde on kamerasta. Se, miten tarkasti etäisyys pitää olla oikea, riippuu sitten eri tekijöistä. Yleisesti tarkkuus on sitä suurempi, mitä pienempi on kohteen etäisyyden suhde polttoväliin, ja mitä suurempi on objektiivin aukko. Aukon vaikutukseen palaa myöhemmissä artikkeleissa.
Olen piirtänyt kuvaan kaksi ”sädettä” kohteena olevan nuolen kärjestä kuvan vastaavaan pisteeseen. Toinen säteistä kulkee pitkin vaakasuoraan linssin keskiakselia, ja taittuu siitä kulkemaan linssin polttopisteen kautta. Toinen puolestaan kulkee linssin keskipisteen kautta muuttamatta suuntaansa. Tällaisella yksinkertaisella geometrisella tarkastelulla voidaan likimääräisesti määrittää kuvan muodostuminen. Ja sen avulla voidaan myös johtaa edellä ollut likimääräinen yhtälö.

Kameran kennon oikea paikka on siis etäisyydellä $s_i$, jonne kuva muodostuu. Kuvaan 4 olen piirtänyt kennon, ja hiukan myös lisää säteitä kulkemaan kohdepisteenä olevasta nuolen kärjestä kennolle muodostuneeseen nuolen kärjen kuvaan. Kun käytetään tätä yksinkertaistettua mallia, niin kaikki nämä säteet risteävät siinä samassa pisteessä. Mutta näin ei siis ole, mikäli linssin toiminta lasketaan tarkasti!
Kuten olen kuvaankin hahmotellut, muodostunut kuva ei ole samankokoinen kuin kohde. On aika helppoa osoittaa yksinkertaisella geometrialla, että kuvan ja kohteen kokojen suhde, eli niin sanottu suurennus, on sama kuin kuvan ja kohteen etäisyyksien suhde – huomioiden, että muodostunut kuva on peilikuva. Eli suurennus $M$ on
$$ M= -\frac{s_i}{s_o} $$
Tässä miinus-merkki kuvaa sitä, että kyseessä on siis peilikuva.
Tähän suurennuksen lausekkeeseen voidaan sitten tietysti sijoittaa kuvan etäisyys linssistä käyttäen aiempaa linssin kuvausyhtälöä. Ja tällöin saadaan esimerkiksi tarkasteltua, miten suurena joku kohde näkyy kameran kennolla, kun käytetään tiettyä polttoväliä, ja kohteella on joku tietty koko.
Linssin kuvausyhtälöllä voimme myös analysoida, mitä tapahtuu silloin, jos kameran edessä on kohteita eri etäisyyksillä – niin kuin niitä tyypillisesti on. Tämän olen hahmotellut kuvaan 5

Kuvassa 5 olen hahmotellut tilanteen, jossa kamera on kohdennettu kohteeseen 1. Eli kennon ja linssin välinen etäisyys on se, jolle kohteen 1 kuva muodostuu, eli $s_{i1}$. Kun sitten kohde 2 on eri etäisyydellä $s_{o2}$ linssistä, niin tämän muodostama kuva onkin terävä etäisyydellä $s_{i2}$; tässä tapauksessa se olisi kauempana kuin $s_{i1}$, koska kohde on lähempänä.
Tämä tarkoittaa sitä, että kun kohteesta 2 lähtevät säteet risteävät vasta kennon takana, niin osuessaan kennoon ne eivät muodostakaan yhtä pistettä, vaan jonkinlaiset isomman valoläiskän. Eli kohteen 2 kuva ei ole terävä. Käyttämällä linssin kuvausyhtälöä ja hiukan geometriaa, voidaan kohtuullisen helposti jopa laskea, kuinka suuri tämä pisteen epäterävä kuva on kennolla.
Kuten kuvaa 5 katsomalla voi jo arvata, sen koko riippuu myös linssin läpimitasta – tai itse asiassa polttovälin ja läpimitan suhteesta eli objektiivin aukkoluvusta. Siksipä palaan tähän aiheeseen myöhemmin jossain toisessa artikkelissa, jossa käsittelen objektiivin aukkoa.
Vaikka linssin kuvausyhtälö antaakin tarkan etäisyyden sille, minne kuva muodostuu, niin se ei siis tarkoita sitä, että vai sillä etäisyydellä olevat kohteet näkyvät terävästi. Aukon ja polttovälin lisäksi tähän vaikuttaa lopulta myös todellisen linssisysteemin kuvausvirheet ja jopa kameran kennon pikseleiden koko. Mutta silti sangen yksinkertainen tarkastelu aukon koko huomioiden kertoo jo paljon siitä, mikä on kuvassa syvyysterävyys.
Kuva-ala
Tämä sama yksinkertainen geometrinen tarkastelu kertoo myös sen, miten laaja on objektiivin näyttämä kuva-ala. Tätä olen hahmotellut kuvassa 6.

Kuten aiemmin hahmottelin yhden kohdepisteen tapauksessa kuvassa 1, yksi geometrinen säde kohteesta kulkee linssin keskipisteen kautta muuttamatta suuntaansa. Kuvaan 6 olen nyt piirtänyt sellaisista kohteen pisteistä nämä yhdet säteet, jotka muodostavat kuvapisteet aivan kameran kennon laidalle.
Jos nämä kohteen pisteet ovat äärettömän kaukana – kuten vaikka tähdet taivaalla – niin kuvan muodostumisetäisyys $s_i$ on sama kuin linssin polttoväli. Tällöin kuvassa 6 näkyvä kulma $\theta$ on helppo ratkaista trigonometrian avulla; se riippuu kennon koosta ja polttovälistä siten, että kulman $\theta$ tangentti on sama kuin kennon koon puolikas jaettuna polttovälillä.
Esimerkiksi tähtitaivasta kuvattaessa voi hyvin helposti tähtikartoista ja muista lähteistä tarkistaa, kuin suurelta alalta tarvitsee ottaa valokuva, jotta saa haluamansa kohteet kuvaan. Ja kun käytössä on joku tietty kamera, jolle kennon koko löytyy spesifikaatioista, saa helposti siis laskettua tuolla, millainen polttoväli tarvitaan objektiiviin, jotta saadaan haluttu kuva.
Useat tähtikuvaajien käyttämät ohjelmistot näyttävät nykyään sen, että jos käyttää tietyn polttovälin objektiivia tai kaukoputkea sen korvikkeena, ja kamera on tietty, niin millaisen kuva-alan se yhdistelmä kattaa taivaalta.
Aivan samoin tämä tietysti toimii myös muussa kuvauksessa. Esimerkiksi jos haluaa ottaa ihmisistä kasvokuvia joiltain tietyiltä etäisyyksiltä, ja kamerassa on tietty kennon koko, voi jo etukäteen laskea ja harkita, että minkä polttovälin objektiivi on tilanteeseen sopiva.
Mutta pieni varoituksen sana laajakulmaisista, lyhyen polttovälin objektiiveista: Tämä edellä kuvattu lasku ei välttämättä anna oikeaa tulosta. Syynä on se, että usein laajakulmaisissa objektiiveissa on vääristymää, jonka seurauksena tuo yksinkertainen malli ei anna aivan oikeaa tulosta. Esimerkiksi kuvan 2 objektiivissa näkyy, että kuvan ideaalisen linssin keskipisteen ja kuvan muodostumispisteen välinen linja ei ole vihreän sädekimpun tapauksessa sama kuin tulevan vihreän sädejoukon tulosuunta ensimmäiselle linssille. Ja tämä on juuri kyseistä vääristymää.
Usein etenkin edullisimmissa laajakulmaisissa linsseissä vääristymää on kuvassa siksi, että se itsessään ei vaikuta kuvan terävyyteen. Silloin objektiivia suunnitellessa hyväksytään vääristymää, koska se usein mahdollistaa paremman kuvan terävyyden kuin mitä saadaan, jos vääristymä yritetään poistaa kokonaan. Ja koska monet kuvankäsittelyohjelmat pystyvät vääristymät, niin niistä ei ole edes pahaa kosmeettista haittaa.
Objektiiveja sitten löytyykin monille eri polttoväleille sen mukaan, mikä on käyttökohde. Ja lisäksi tietysti myös zoom-objektiiveja, joissa tämä yksinkertaistetun mallin polttoväli on muuttuva. Mutta näistä kerron sitten ehkä myöhemmin.
Tilt/shift – objektiivit
Otanpa vielä yhden vähän harvinaisemman tapauksen objektiivit käsittelyyn – koska näidenkin periaate hoituu samalla yksinkertaisella kuvausyhtälöllä. Kyseessä ovat niin sanotut tilt/shift – objektiivit.
Näissä objektiiveissa on kyse siitä, että niiden linssiä voidaan joko siirtää poikittaisessa suunnassa (shift) tai kallistaa vinoon (tilt). Tarkastellaan näistä ensin hiukan shift-tapausta.
Kuvattaessa joko ylä- tai alaviistoon, kuvissa tulee normaalisti näkyviin perspektiivivirhettä. Esimerkiksi siis jos halutaan ottaa valokuva korkeasta rakennuksesta läheltä siten, että kamera kallistetaan osoittamaan yläviistoon.
Yhdistämällä linssin kuvausyhtälö ja suurennuksen lauseke nähdään heti, että tällöin alaosalle rakennusta (joka on lähempänä kameraa) suurennus on suurempi kuin rakennuksen yläosa (joka on kauempana kamerasta). Ja tällöin pystysuorat linjat näyttävät ”kaatuvan” kohti kuvan keskustaa. Ja jos ottaa kuvan metsän puista yläviistoon, niin reunalla olevat puut näyttävät olevan hyvinkin vinossa. Tämän virheen saa kyllä nykyään korjattua monissa valokuvausohjelmistoissa, mutta aina on parempi, jos alkuperäisessä kuvassa ei ole virhettä, koska muokkaaminen aina heikentää laatua muutenkin.
Tätä perspektiivivirhettä ei tule silloin, jos kameran linssin ja kennon linja on kohtisuorassa kuvattavaan kohteeseen. Eli jos menee tarpeeksi kauaksi kohteesta siten, että korkea kohde mahtuu kuvaan vaikka tämä linja on kohtisuorassa, niin perspektiivi tulee oikein. Mutta korkeiden kohteiden tapauksessa tämä ei välttämättä ole käytännöllistä, koska silloin kuvan alaosaan jää paljon turhaa alaa, jonka joutuu leikkaamaan pois.
Shift-objektiivissa tämä poisleikkaamisen tarve poistuu. Tämä perustuu hyvin yksinkertaiseen periaatteeseen – siirretään kameran kennoa suhteessa linssiin, kuten olen hahmotellut kuvassa 7.
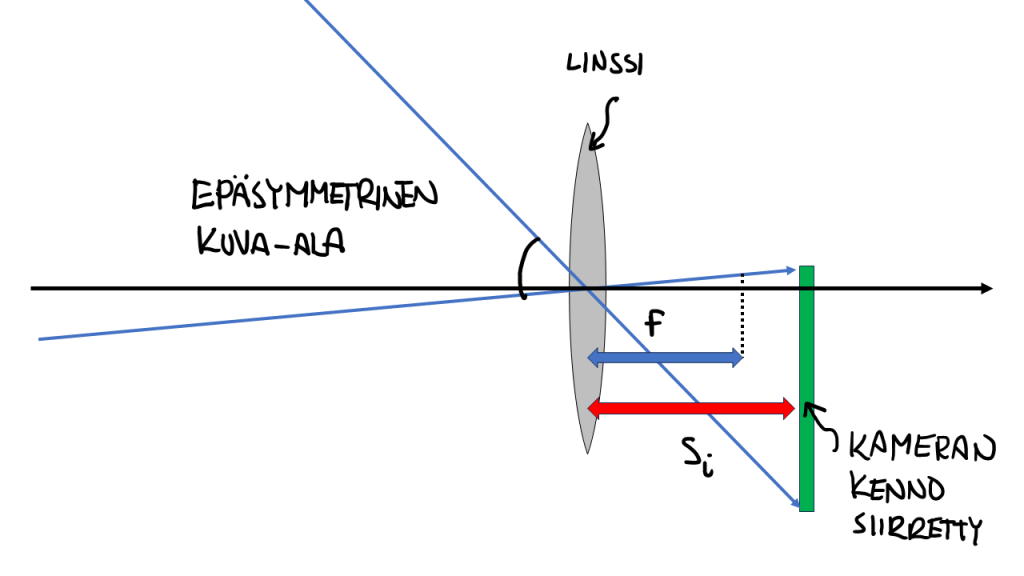
Tällöin jos piirtää kennon nurkkiin säteet linssin keskipisteen kautta, niin näkee, että kuva-ala siirtyy samalla, mutta linssin normaalin suunta säilyy edelleen muuttumattomana. Tämä säilyttää perspektiivin, mutta kameran kuvan keskikohta siirtyy ylöspäin, ja saadaan kuvaan vaikka se korkea rakennus.
Käytännössä ei kamerassa siirretä kennoa, vaan objektiivissa on mekaniikkaa, joka siirtää linssiä suhteessa kennoon. Mutta tällä toteutuksella ei ole merkitystä lopputulokselle.
Objektiiveissa, joissa tämä siirto, ”shift,” on mahdollista, on yleensä myös mahdollisuus kallistaa linssiä suhteessa kennoon; tätä olen hahmotellut kuvassa 8.
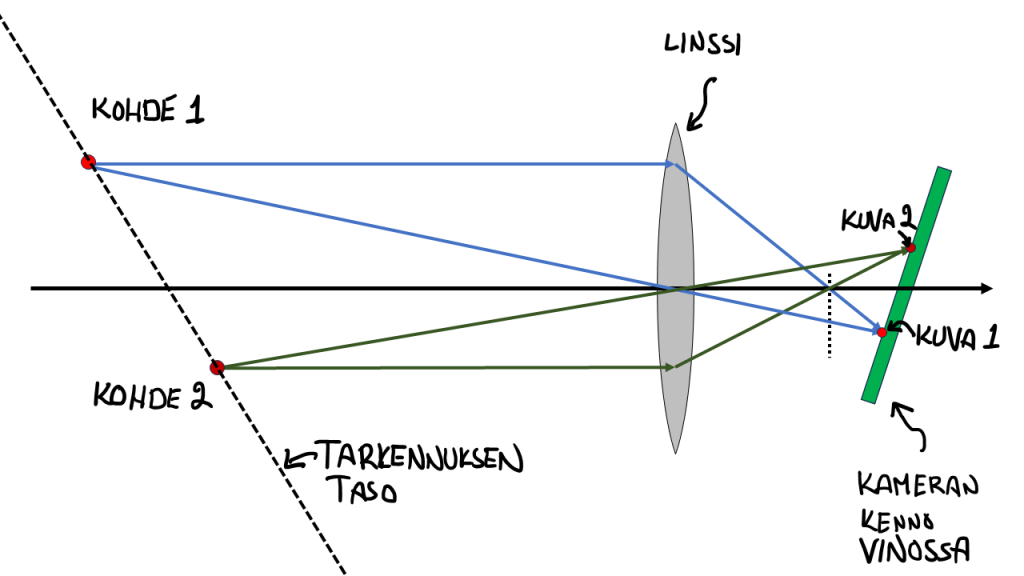
Jälleen voimme käyttää samaa linssin kuvausyhtälöä, tai vaihtoehtoisesti piirtää kuvaan taas geometrisia säteitä. Kuvaan olen piirtänyt kahteen eri kuvapisteisiin kumpaankin säteet, jotka tulevat kohtisuoraan linssille ja siitä polttopisteen kautta kennolle, ja toiset linssin keskipisteen kautta.
Tällainen hyvin yksinkertainen tarkastelu näyttää sen, että jos kenno on vinossa suhteessa linssiin, niin tarkennus tapahtuu vinolle tasolle. Tällaiselle voi käyttöä silloin, kun pitää saada joku vino kohde tarkennettua. Tai jos halutaan tehdä jotain taiteellisia vaikutelmia tarkennuksen kanssa.
Loppusanat
Kaikki optiikassa ei ole hirvittävän monimutkaista matematiikkaa. Käytännössä käytin tämän koko tarinan taustalla vain yhtä yhtälöä. Ja silti pystyn aika paljon asioita kertomaan ja perustelemaan tämän yhden yhtälön avulla.
Toki sitten kun lähdetään oikeasti suunnittelemaan ja analysoimaan objektiiveja, niin tarvitaan jo hiukan järeämpiä työkaluja. Näistä kerron ehkä joskus myöhemmin.
Mutta seuraavaksi aion puhua objektiivin aukosta. Sillä kun on hyvin paljon merkitystä kuvaan.

